The Math Behind The Shockingly Simple Math Behind Early Retirement
This site utilizes Google Analytics, Google AdSense, as well as participates in affiliate partnerships with various companies including Amazon. Please view the privacy policy for more details.
One of the more popular articles in the financial independence blogosphere is Mr. Money Mostache’s The Shockingly Simple Math Behind Early Retirement. If you haven’t read it, check it out. While I found it interesting, I think that the simple math is lacking, well, math, so I wanted to dig a bit deeper and figure out where the numbers came from.
I’m not the first to have done this. Early Retirement Now examined it in the article The Shockingly Simple/Complicated/Random Math Behind Saving For Early Retirement. Go Curry Cracker examined it in the article Financial Independence: How Long Will It Take?. Both took an empirical approach.
I’m taking a different approach and looking just at equations.
It turns out that the “shockingly simple” math is based on these two equations:
income = expenses + savings
FV = PMT(1 + i)[((1+i)^n-1)/(i)]
That second equation is known as the annuity formula, a variant of the compound interest formula that only takes into account contributions (or payments) and assumes the interest rate period is equal to the payment/contribution period.
Note: FV is final value, PMT is payment (or contribution, in the case of investments), i is the interest rate for the period, and n is the number of periods.
A normal rule of thumb for retirement is known as the 4% rule. That means you need 25 times your annual expenses to live indefinitely just from your investments. Why 25 times? First, 25 is the reciprocal of 4% (i.e., 1/0.04). It assumes you’re living off an investment that makes 4% or more.
The 4% rule means we need the final value to be 25 times our expenses. Our contributions are our savings. Let’s plug these values into the equation:
25 * expenses = savings (1 + i) [((1+i)^n-1)/(i)]
Mr. Money Moustache assumes a 5% return, so let’s plug that value in:
25 * expenses = savings (1 + 0.05) [((1 + 0.05)^n-1)/(0.05)]
Now let’s solve for n (hopefully without doing multiple steps at once :)):
25 * expenses = savings (1 + 0.05) [((1 + 0.05)^n-1)/(0.05)]
25 * expenses = savings (1.05) [((1.05)^n-1)/(0.05)]
(25 * expenses) / (1.05 * savings) = ((1.05)^n-1)/0.05
0.05 * (25 * expenses) / (1.05 * savings) = ((1.05)^n-1)/0.05
(1.25 * expenses) / (1.05 * savings) = (1.05)^n-1
[(1.25 * expenses) / (1.05 * savings)] + 1 = (1.05)^n
log([(1.25 * expenses) / (1.05 * savings)] + 1) = log((1.05)^n)
log([(1.25 * expenses) / (1.05 * savings)] + 1) = n * log(1.05)
log([(1.25 * expenses) / (1.05 * savings)] + 1) / log(1.05) = n
n = log([(1.25 * expenses) / (1.05 * savings)] + 1) / log(1.05)
Note: It shouldn’t matter what type of logarithm you use - base 10, natural, base 2, base π, or any other - so long as you use the same one for both sides.
Now we just need to reconstruct the table. But how do we do that if we don’t know what expense are? After all, he just uses savings rate in his table!
Remember, savings and expenses have a relationship that we already expressed earlier:
income = expenses + savings
This means the higher the savings rate, the lower the expenses, assuming income stays still. And here’s a fun fact: you can control the equation variables by expressing it in terms of percentage:
100% of your income = expense rate % + savings rate %
This explains why, if you’re able to save 100% of your income, then you can retire right now: you have no expenses!
Let’s try plugging the numbers in to see if I get the same results Mr. Money Mostache did:
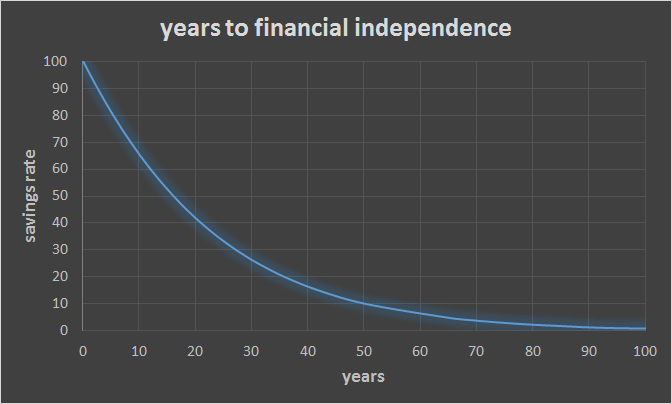
| expenses | savings | years |
|---|---|---|
| 100 | 0 | — |
| 95 | 5 | 64.8 |
| 90 | 10 | 50.4 |
| 85 | 15 | 42.0 |
| 80 | 20 | 35.9 |
| 75 | 25 | 31.2 |
| 70 | 30 | 27.2 |
| 65 | 35 | 23.9 |
| 60 | 40 | 21.0 |
| 55 | 45 | 18.4 |
| 50 | 50 | 16.1 |
| 45 | 55 | 13.9 |
| 40 | 60 | 12.0 |
| 35 | 65 | 10.2 |
| 30 | 70 | 8.4 |
| 25 | 75 | 6.8 |
| 20 | 80 | 5.3 |
| 15 | 85 | 3.9 |
| 10 | 90 | 2.5 |
| 5 | 95 | 1.2 |
| 0 | 100 | 0 |
Note: I made this table in Excel. Each row looks something like this:
=A2-5=100-A3=LOG10(((1.25 * A3) / (1.05 * B3)) + 1) /LOG10(1.05)except the first row, since it will result in a divide by zero error.
My numbers are slightly different. My guess would be either he had multiple interest periods annually (versus my one) or that fact that his assumption of 5% returns included being adjusted for inflation.
Lastly, one nice thing about this math is that it isn’t linear - it has a nice curve to it. Check out this chart:
2 comments for The Math Behind The Shockingly Simple Math Behind Early Retirement
Leave a Reply
Nice analysis! The math behind this gets tricky fast. I tried to do the math around this same analysis but adding on the idea:
That makes the math MUCH harder. I know that would lower these times, but I’m unsure of how much that’d impact things. It would impact the lowest saving rate people the most, but be interesting to see how it impacts people in the middle range.
At that point, I’m not sure it could be solved in a single equation, although I could see something along the lines of how long would it take you to reach a certain savings rate. For instance, if your income currently equals you expenses (i.e. a savings rate of 0%) how long would it take to reach a 50% savings rate if you get a 3% raise every year and save it?
I just did a quick excel sheet, and the answer to that question that looks like around 24 years:
Reply to This Thread