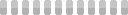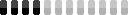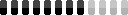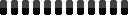3D Colorspace Geometry

March 1, 2021

This site utilizes Google Analytics, Google AdSense, as well as participates in affiliate partnerships with various companies including Amazon. Please view the privacy policy for more details.

When most people think of three dimensions, they think of three positional (spatial) dimensions. Up & down, left & right, forward & back. I was thinking - instead of a positional dimension, what if we used something else that we can perceive such as color?

I decided to call this combination of color and space colorspace.

In this sense, the single word colorspace is analogous to spacetime rather than the two-word term color space meaning how to organize colors.

Maybe I should’ve called it spacecolor, but that doesn’t roll off the tongue quite the same, and I digress.

My initial thought was to apply this to three-dimensional objects to see what their four-dimensional counterparts would look like. For instance, I could construct a cube and color it to make it a tesseract. Instead, I simplified things and applied the concept to two-dimensional objects by adding a third color dimension.

The Representation

I represented the shapes in a three-dimensional array of the first octant of a 3D coordinate system.

An octanct is merely the 3D counterpart to the 2D quadrant. So the 2D equivalent of, say, a filled-in square would look something like this:

A 3D filled-in cube would of similar dimensions would consist of five layers:

The first layer would be empty:

The second through fourth layers would be:

And the final, fifth layer would be empty:

Note that this is a horrible, memory-inefficient way to store the data.

The Tests

I decided to make my images on a 256 × 256 × 256 canvas.

That’s an HTML Canvas where each canvas is 256 pixels wide and 256 pixels tall. Each pixel can be one of 256 gray colors - including black and white.

Wait, shouldn’t there be 256 bits of color? Well, yeah, but the normal RGB colors are only 24 bits - 8 bits for each color. “Normally” with 24 bits there are 2^24 colors, or 16,777,216 colors. With 256 bits, that’s enough for 2^256 colors, or 115,792,089,237,316,195,423,570,985,008,687,907,853,269,984,665,640,564,039,457,584,007,913,129,639,936 colors. I don’t even know how to pronounce that number.

The gray color is specified by the topmost color coordinate. So if there is no color coordinate in a given (x,y) coordinate, then the color is 000000 - black. If the very tippy top coordinate in a given (x,y) coordinate has a value, then the color is FFFFFF - white. If, say, the 127th is the “topmost” then the color is 747474.

Here’s a 256 × 10 canvas representation of all the colors, along with the JavaScript necessary to make the colors:

And here’s an empty 256 × 256 (i.e. black) canvas, along with the JavaScript to make said canvas:

Note: the let functions = [grays] and functions.push(empty) at the end of each script tag allow me to defer the execution until later.

And now I will show a sphere and three instances of a cube:

A Sphere

A Cube - But Staring Straight On

A Rotated Cube - But Still Staring Straight On

A Cube Rotated 45 on All Three Axis

The Deferred Execution

Execution is deferred so I can have the following style tag applied first:

And then execute:

Final Comments

Interestingly enough, when more than one color depth was visible, it appeared, at least to me, to be three-dimensional in the “normal” three spatial dimensions.

Making something darker the further away it is isn’t a new 3D graphics technique. In this basic ray caster demo on Mozilla’s website, the author notes that they “blended with a darker version of the color according to the distance to the wall” almost in passing, as if it’s common knowledge.

So, yeah, nothing new there.